LEYES DE NEWTON, EQUILIBRIO, TRABAJO, ENERGÍA Y POTENCIA.
1.-DEFINIRÁ LAS TRES LEYES DE NEWTON
2.-PROBLEMAS APLICADOS A LAS LEYES DE NEWTON
3.-EXPLICARA LA PRIMERA CONDICIÓN DE EQUILIBRIO.
4.-PROBLEMAS APLICANDO LA PRIMERA CONDICIÓN DE EQUILIBRIO
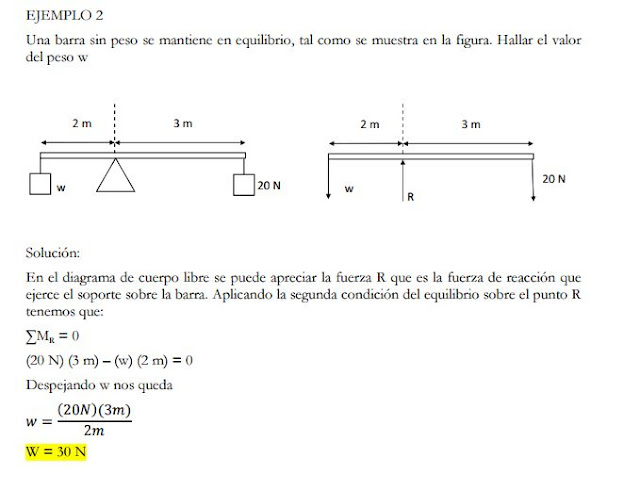
5.-EXPLICARA LA SEGUNDA CONDICIÓN DE EQUILIBRIO.
6.-PROBLEMAS APLICANDO LA SEGUNDA CONDICIÓN DE EQUILIBRIO.
7.-EXPLICARA EL ROZAMIENTO O FRICCIÓN.
8.-DEFINIRÁ TRABAJO, ENERGÍA Y POTENCIA.
9.-PROBLEMAS SOBRE TRABAJO ENERGÍA Y POTENCIA.
1.-DEFINIRÁ LAS TRES LEYES DE NEWTON
Las leyes de Newton, también conocidas como leyes del movimiento de Newton,son tres principios a partir de los cuales se explican la mayor parte de los problemas planteados por la mecánica, en particular aquellos relativos al movimiento de los cuerpos, que revolucionaron los conceptos básicos de la física y el movimiento de los cuerpos en el universo.
Constituyen los cimientos no solo de la dinámica clásica sino también de la física clásica en general. Aunque incluyen ciertas definiciones y en cierto sentido pueden verse como axiomas, Newton afirmó que estaban basadas en observaciones y experimentos cuantitativos; ciertamente no pueden derivarse a partir de otras relaciones más básicas. La demostración de su validez radica en sus predicciones... La validez de esas predicciones fue verificada en todos y cada uno de los casos durante más de dos siglos.
En concreto, la relevancia de estas leyes radica en dos aspectos: por un lado constituyen, junto con la transformación de Galileo, la base de la mecánica clásica, y por otro, al combinar estas leyes con la ley de la gravitación universal, se pueden deducir y explicar las leyes de Kepler sobre el movimiento planetario. Así, las leyes de Newton permiten explicar, por ejemplo, tanto el movimiento de los astros como los movimientos de los proyectiles artificiales creados por el ser humano y toda la mecánica de funcionamiento de las máquinas. Su formulación matemática fue publicada por Isaac Newton en 1687 en su obra Philosophiæ naturalis principia mathematica.
La dinámica de Newton, también llamada dinámica clásica, solo se cumple en los sistemas de referencia inerciales (que se mueven a velocidad constante; la Tierra, aunque gire y rote, se trata como tal a efectos de muchos experimentos prácticos). Solo es aplicable a cuerpos cuya velocidad dista considerablemente de la velocidad de la luz; cuando la velocidad del cuerpo se va aproximando a los 300 000 km/s (lo que ocurriría en los sistemas de referencia no-inerciales) aparecen una serie de fenómenos denominados efectos relativistas. El estudio de estos efectos (aumento de la masa y contracción de la longitud, fundamentalmente) corresponde a la teoría de la relatividad especial, enunciada por Albert Einstein en 1905.
Primera ley de Newton o ley de inercia
La primera ley del movimiento rebate la idea aristotélica de que un cuerpo solo puede mantenerse en movimiento si se le aplica una fuerza. Newton expone que:
Esta ley postula, por tanto, que un cuerpo no puede cambiar por sí solo su estado inicial, ya sea en reposo o en movimiento rectilíneo uniforme, a menos que se aplique una fuerza o una serie de fuerzas cuya resultante no sea nula. Newton toma en consideración, así, el que los cuerpos en movimiento están sometidos constantemente a fuerzas de roce o fricción, que los frena de forma progresiva, algo novedoso respecto de concepciones anteriores que entendían que el movimiento o la detención de un cuerpo se debía exclusivamente a si se ejercía sobre ellos una fuerza, pero nunca entendiendo como tal a la fricción.
En consecuencia, un cuerpo que se desplaza con movimiento rectilíneo uniforme implica que no existe ninguna fuerza externa neta o, dicho de otra forma, un objeto en movimiento no se detiene de forma natural si no se aplica una fuerza sobre él. En el caso de los cuerpos en reposo, se entiende que su velocidad es cero, por lo que si esta cambia es porque sobre ese cuerpo se ha ejercido una fuerza neta.
Newton descubrió la ley de la inercia, la tendencia de un objeto en movimiento a continuar moviéndose en una línea recta, a menos que sufra la influencia de algo que le desvíe de su camino. Newton supuso que si la Luna no salía disparada en línea recta, según una línea tangencial a su órbita, se debía a la presencia de otra fuerza que la empujaba en dirección a la Tierra, y que desviaba constantemente su camino convirtiéndolo en un círculo. Newton llamó a esta fuerza gravedad y creyó que actuaba a distancia. No hay nada que conecte físicamente la Tierra y la Luna y sin embargo la Tierra está constantemente tirando de la Luna hacia nosotros. Newton se sirvió de la tercera ley de Kepler y dedujo matemáticamente la naturaleza de la fuerza de la gravedad. Demostró que la misma fuerza que hacía caer una manzana sobre la Tierra mantenía a la Luna en su órbita.
La primera ley de Newton establece la equivalencia entre el estado de reposo y de movimiento rectilíneo uniforme. Supongamos un sistema de referencia S y otro S´ que se desplaza respecto del primero a una velocidad constante. Si sobre una partícula en reposo en el sistema S´ no actúa una fuerza neta, su estado de movimiento no cambiará y permanecerá en reposo respecto del sistema S´ y con movimiento rectilíneo uniforme respecto del sistema S. La primera ley de Newton se satisface en ambos sistemas de referencia. A estos sistemas en los que se satisfacen las leyes de Newton se les da el nombre de sistemas de referencia inerciales. Ningún sistema de referencia inercial tiene preferencia sobre otro sistema inercial, son equivalentes: este concepto constituye el principio de relatividad de Galileo o newtoniano.
El enunciado fundamental que podemos extraer de la ley de Newton es que la . Esta expresión es una ecuación vectorial, ya que tanto la fuerza como la aceleración llevan dirección y sentido. Por otra parte, cabe destacar que la aceleración no es la variación de la posición, sino que es la variación con la que varía la velocidad.
De la ecuación podemos deducir que si actúan fuerzas sobre los cuerpos, el cambio que se provoca en su aceleración es proporcional a la fuerza aplicada y dicho cambio se produce en la dirección sobre la que se apliquen dichas fuerzas.
Segunda ley de Newton o ley fundamental de la dinámica
La Segunda Ley de Newton expresa que:
Esta ley se encarga de cuantificar el concepto de fuerza. La aceleración que adquiere un cuerpo es proporcional a la fuerza neta aplicada sobre el mismo. La constante de proporcionalidad es la masa del cuerpo (que puede ser o no ser constante). Entender la fuerza como la causa del cambio de movimiento y la proporcionalidad entre la fuerza impresa y el cambio de la velocidad de un cuerpo es la esencia de esta segunda ley.
Si la masa es constante
Si la masa del cuerpo es constante se puede establecer la siguiente relación, que constituye la ecuación fundamental de la dinámica:
Donde m es la masa del cuerpo la cual debe ser constante para ser expresada de tal forma. La fuerza neta que actúa sobre un cuerpo, también llamada fuerza resultante, es el vector suma de todas las fuerzas que sobre él actúan. Así pues:
- La aceleración que adquiere un cuerpo es proporcional a la fuerza aplicada, y la constante de proporcionalidad es la masa del cuerpo.
- Si actúan varias fuerzas, esta ecuación se refiere a la fuerza resultante, suma vectorial de todas ellas.
- Esta es una ecuación vectorial, luego se debe cumplir componente a componente.
- En ocasiones será útil recordar el concepto de componentes intrínsecas: si la trayectoria no es rectilínea es porque hay una aceleración normal, luego habrá también una fuerza normal (en dirección perpendicular a la trayectoria); si el módulo de la velocidad varía es porque hay una aceleración en la dirección de la velocidad (en la misma dirección de la trayectoria).
- La fuerza y la aceleración son vectores paralelos, pero esto no significa que el vector velocidad sea paralelo a la fuerza. Es decir, la trayectoria no tiene por qué ser tangente a la fuerza aplicada (sólo ocurre si al menos, la dirección de la velocidad es constante).
- Esta ecuación debe cumplirse para todos los cuerpos. Cuando analicemos un problema con varios cuerpos y diferentes fuerzas aplicadas sobre ellos, deberemos entonces tener en cuenta las fuerzas que actúan sobre cada uno de ellos y el principio de superposición de fuerzas. Aplicaremos la segunda ley de Newton para cada uno de ellos, teniendo en cuenta las interacciones mutuas y obteniendo la fuerza resultante sobre cada uno de ellos.
El principio de superposición establece que si varias fuerzas actúan igual o simultáneamente sobre un cuerpo, la fuerza resultante es igual a la suma vectorial de las fuerzas que actúan independientemente sobre el cuerpo (regla del paralelogramo). Este principio aparece incluido en los Principia de Newton como Corolario 1, después de la tercera ley, pero es requisito indispensable para la comprensión y aplicación de las leyes, así como para la caracterización vectorial de las fuerzas. La fuerza modificará el estado de movimiento, cambiando la velocidad en módulo o dirección. Las fuerzas son causas que producen aceleraciones en los cuerpos. Por lo tanto existe una relación causa-efecto entre la fuerza aplicada y la aceleración que se este cuerpo experimenta.
De esta ecuación se obtiene la unidad de medida de la fuerza en el Sistema Internacional de Unidades, el Newton:
Por otro lado, si la fuerza resultante que actúa sobre una partícula no es cero, esta partícula tendrá una aceleración proporcional a la magnitud de la resultante y en dirección de esta (debido a que la masa siempre es un escalar positivo). La expresión anterior así establecida es válida tanto para la mecánica clásica como para la mecánica relativista (la dinámica clásica afirma que la masa de un cuerpo es siempre la misma, con independencia de la velocidad con la que se mueve, la mecánica relativista establece que la masa de un cuerpo aumenta al crecer la velocidad).
Si la masa no es constanteSi la masa de los cuerpos varia, como por ejemplo un cohete que va quemando combustible, no es válida la relación y hay que hacer genérica la ley para que incluya el caso de sistemas en los que pueda variar la masa. Para ello primero hay que definir una magnitud física nueva, la cantidad de movimiento, que se representa por la letra p y que se define como el producto de la masa de un cuerpo por su velocidad, es decir:
Newton enunció su ley de una forma más general:
De esta forma se puede relacionar la fuerza con la aceleración y con la masa, sin importar que esta sea o no sea constante. Cuando la masa es constante sale de la derivada con lo que queda la expresión:
Y se obtiene la expresión clásica de la Segunda Ley de Newton:
La fuerza, por lo tanto, es un concepto matemático el cual, por definición, es igual a la derivada con respecto al tiempo del momento de una partícula dada, cuyo valor a su vez depende de su interacción con otras partículas. Por consiguiente, se puede considerar la fuerza como la expresión de una interacción. Otra consecuencia de expresar la Segunda Ley de Newton usando la cantidad de movimiento es lo que se conoce como principio de conservación de la cantidad de movimiento: si la fuerza total que actúa sobre un cuerpo es cero, la Segunda ley de Newton nos dice que
Tercera ley de Newton o principio de acción y reacción
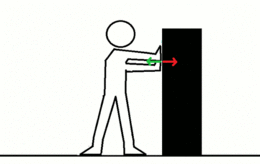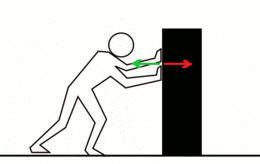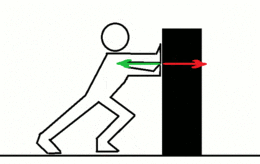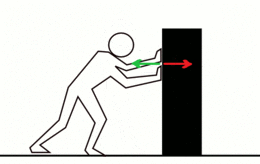
La tercera ley de Newton establece lo siguiente: siempre que un objeto ejerce una fuerza sobre un segundo objeto, este ejerce una fuerza de igual magnitud y dirección pero en sentido opuesto sobre el primero. Con frecuencia se enuncia así: A cada acción siempre se opone una reacción igual pero de sentido contrario. En cualquier interacción hay un par de fuerzas de acción y reacción situadas en la misma dirección con igual magnitud y sentidos opuestos. La formulación original de Newton es:
Esta tercera ley de Newton es completamente original (pues las dos primeras ya habían sido propuestas de otra manera por Galileo, Hooke y Huygens) y hace de las leyes de lamecánica un conjunto lógico y completo. Expone que por cada fuerza que actúa sobre un cuerpo, este realiza una fuerza de igual intensidad, pero de sentido contrario sobre el cuerpo que la produjo. Dicho de otra forma, las fuerzas, situadas sobre la misma recta, siempre se presentan en pares de igual magnitud y de dirección, pero con sentido opuesto. Si dos objetos interaccionan, la fuerza F12, ejercida por el objeto 1 sobre el objeto 2, es igual en magnitud con misma dirección pero sentidos opuestos a la fuerza F21 ejercida por el objeto 2 sobre el objeto 1:
Este principio presupone que la interacción entre dos partículas se propaga instantáneamente en el espacio (lo cual requeriría velocidad infinita), y en su formulación original no es válido para fuerzas electromagnéticas puesto que estas no se propagan por el espacio de modo instantáneo sino que lo hacen a velocidad finita "c". Este principio relaciona dos fuerzas que no están aplicadas al mismo cuerpo, produciendo en ellos aceleraciones diferentes, según sean sus masas. Por lo demás, cada una de esas fuerzas obedece por separado a la segunda ley. Junto con las anteriores leyes, esta permite enunciar los principios de conservación del momento lineal y del momento angular.
Aplicaciones de la Tercera Ley de Newton
Algunos ejemplos donde actúan las fuerzas acción-reacción son los siguientes:
- Si una persona empuja a otra de peso similar, las dos se mueven con la misma velocidad pero en sentido contrario.
- Cuando saltamos, empujamos a la tierra hacia abajo, que no se mueve debido a su gran masa, y esta nos empuja con la misma intensidad hacia arriba.
- Una persona que rema en un bote empuja el agua con el remo en un sentido y el agua responde empujando el bote en sentido opuesto.
- Cuando caminamos empujamos a la tierra hacia atrás con nuestros pies, a lo que la tierra responde empujándonos a nosotros hacia delante, haciendo que avancemos.
- Cuando se dispara una bala, la explosión de la pólvora ejerce una fuerza sobre la pistola (que es el retroceso que sufren las armas de fuego al ser disparadas), la cual reacciona ejerciendo una fuerza de igual intensidad pero en sentido contrario sobre la bala.
- La fuerza de reacción que una superficie ejerce sobre un objeto apoyado en ella, llamada fuerza normal con dirección perpendicular a la superficie.
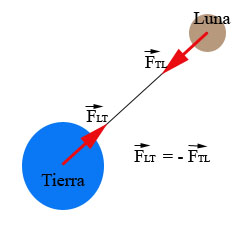
- Las fuerzas a distancia no son una excepción, como la fuerza que la Tierra ejerce sobre la Luna y viceversa, su correspondiente pareja de acción y reacción:
La fuerza que ejerce la Tierra sobre la Luna es exactamente igual (y de signo contrario) a la que ejerce la Luna sobre la Tierra y su valor viene determinado por la ley de gravitación universal enunciada por Newton, que establece que la fuerza que ejerce un objeto sobre otro es directamente proporcional al producto de sus masas, e inversamente proporcional al cuadrado de la distancia que los separa. La fuerza que la Tierra ejerce sobre la Luna es la responsable de que esta no se salga de su órbita circular.
Además, la fuerza que la Luna ejerce sobre la Tierra es también responsable de las mareas, pues conforme la Luna gira alrededor de la Tierra esta ejerce una fuerza de atracción sobre la superficie terrestre, la cual eleva los mares y océanos, elevando varios metros el nivel del agua en algunos lugares; por este motivo esta fuerza también se llama fuerza de marea. La fuerza de marea de la luna se compone con la fuerza de marea del sol proporcionando el fenómeno completo de las mareas.
PROBLEMAS DE LAS LEYES DE NEWTON
Ejemplo de problemas relacionados con la Segunda Ley de Newton.
- 1. Una fuerza le proporciona a la masa de 2,5 Kg. una aceleración de 1,2 m/s2. Calcular la magnitud de dicha fuerza en Newton y dinas.
Datos
m = 2,5 Kg.
a =1,2 m/s2.
F =? (N y dyn)
Solución
Nótese que los datos aparecen en un mismo sistema de unidades (M.K.S.)
Para calcular la fuerza usamos la ecuación de la segunda ley de Newton:
Como nos piden que lo expresemos en dinas, bastará con multiplicar por 105, luego:
- 2. ¿Qué aceleración adquirirá un cuerpo de 0,5 Kg. cuando sobre él actúa una fuerza de 200000 dinas?
Datos
a =?
m = 2,5 Kg.
F = 200000 dyn
Solución
La masa está dada en M.K.S., en cambio la fuerza está dada en c.g.s.
Para trabajar con M.K.S. debemos transformar la fuerza a la unida M.K.S. de esa magnitud (N)

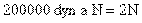
La ecuación de la segunda ley de Newton viene dada por:
- 3. Un cuerpo pesa en la tierra 60 Kp. ¿Cuál será a su peso en la luna, donde la gravedad es 1,6 m/s2?
Datos
PT= 60 Kp = 588 N
PL =?
gL = 1,6 m/s2
Solución
Para calcular el peso en la luna usamos la ecuación
Como no conocemos la masa, la calculamos por la ecuación: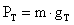 que al despejar m tenemos:
que al despejar m tenemos:
Esta masa es constante en cualquier parte, por lo que podemos usarla en la ecuación (I):

- 4. Un ascensor pesa 400 Kp. ¿Qué fuerza debe ejercer el cable hacia arriba para que suba con una aceleración de 5 m/s2? Suponiendo nulo el roce y la masa del ascensor es de 400 Kg.
Solución
Como puede verse en la figura 7, sobre el ascensor actúan dos fuerzas: la fuerza F de tracción del cable y la fuerza P del peso, dirigida hacia abajo.
La fuerza resultante que actúa sobre el ascensor es F – P
Aplicando la ecuación de la segunda ley de Newton tenemos:
Al transformar 400 Kp a N nos queda que:
400 Kp = 400 ( 9,8 N = 3920 N
Sustituyendo los valores de P, m y a se tiene:
F – 3920 N = 400 Kg. ( 0,5 m/s2
F – 3920 N = 200 N
Si despejamos F tenemos:
F = 200 N + 3920 N
F = 4120 N
- 5. Un carrito con su carga tiene una masa de 25 Kg. Cuando sobre él actúa, horizontalmente, una fuerza de 80 N adquiere una aceleración de 0,5 m/s2. ¿Qué magnitud tiene la fuerza de rozamiento Fr que se opone al avance del carrito?
Solución
En la figura 8 se muestran las condiciones del problema
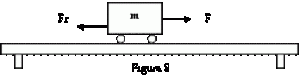
La fuerza F, que actúa hacia la derecha, es contrarrestada por la fuerza de roce Fr, que actúa hacia la izquierda. De esta forma se obtiene una resultante F – Fr que es la fuerza que produce el movimiento.
Si aplicamos la segunda ley de Newton se tiene:
Sustituyendo F, m y a por sus valores nos queda
80 N – Fr = 25 Kg. ( 0,5 m/s2
80 N – Fr = 12,5 N
Si despejamos Fr nos queda:
Fr = 80 N – 12,5 N
Fr = 67,5 N
- 6. ¿Cuál es la fuerza necesaria para que un móvil de 1500 Kg., partiendo de reposo adquiera una rapidez de 2 m/s2 en 12 s?
Datos
F =?
m = 1500 Kg.
Vo = 0
Vf = 2 m/s2
t = 12 s
Solución
Como las unidades están todas en el sistema M.K.S. no necesitamos hacer transformaciones.
De esa ecuación conocemos la masa, pero desconocemos la aceleración. Esta podemos obtenerla a través de la ecuación
Porque partió de reposo.
Sustituyendo Vf y t por sus valores tenemos:
Si sustituimos el valor de a y de m en la ecuación (I) tenemos que:

- 7. Calcular la masa de un cuerpo, que estando de reposo se le aplica una fuerza de 150 N durante 30 s, permitiéndole recorrer 10 m. ¿Qué rapidez tendrá al cabo de ese tiempo?
Datos
m =?
Vo = 0
F = 150 N
t = 30 s
x = 10 m
Vf =?
Solución
Como nos piden la masa, despejamos la segunda la segunda ley de Newton:

Como no se conoce la aceleración y nos dan la distancia que recorre partiendo de reposo, usamos la ecuación de la distancia en función del tiempo y despejamos (a)
Sustituyendo valores tenemos:
Sustituyendo los valores de X y t en (II) tenemos:
Tercera ley de newton.
- 1. Consideramos un cuerpo con un masa m = 2 Kg. que está en reposo sobre un plano horizontal, como el indicado en la figura 17. a) Haz un diagrama de cuerpo libre. b) Calcular la fuerza con que el plano reacciona contra el bloque.

Solución
a) Las fuerzas que actúan sobre el bloque están representadas en la figura 18, donde se elije un eje de coordenadas cuyo origen es el centro del cuerpo, mostrándose las fuerzas verticales: el peso y la normal
y la normal 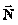
 y la normal
y la normal 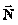
Al diagrama así mostrado se le llama diagrama de cuerpo libre.
b) Para calcular la fuerza que el plano ejerce sobre el bloque aplicamos la segunda ley de Newton:
Como  actúa hacia arriba y
actúa hacia arriba y 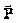 actúa hacia abajo, la resultante viene dada en módulo por N – P, que al aplicar la segunda ley de Newton escribimos:
actúa hacia abajo, la resultante viene dada en módulo por N – P, que al aplicar la segunda ley de Newton escribimos:
N – P = m . a
Como en la dirección vertical no hay movimiento entonces la aceleración es cero (a = 0), luego
N – P = 0
N = P
N = m . g (porque P = m ( g)
Sustituyendo los valores de m y g se tiene:
N = 2 Kg . 9,8 m/s2
N = 19,6 N
Esta es la fuerza con que el plano reacciona sobre el bloque.
- 2. En la figura 19 se muestran dos masas M1 = 3 Kg. y M2 = 5 Kg. colgando de los extremos de un hilo que pasa por la garganta de una polea a) Hacer un diagrama de las fuerzas que actúan b) Calcular la tensión del hilo y la aceleración con que se mueve el sistema.
Solución
a) Obsérvese la figura 20(a), la cual representa el diagrama del cuerpo libre para el cuerpo de masa M1.
En la figura 20(b) se muestra el diagrama de cuerpo libre para el cuerpo de masa M2.
b) Como el cuerpo de masa M1 sube, la tensión T es mayor que P, por lo que podemos escribir en módulo la segunda ley de Newton así:
T – P1 = M1 . a.………………………………………… (A)
Como el cuerpo de masa M2 baja, el peso P2 es mayor que T, pudiéndose escribir en módulo la segunda ley de Newton así:
P2 – T = M2 . a.………………………………………… (B)
Despajando T de la ecuación (A) nos queda que:
T = M1 . a + P1
Sustituyendo ésta expresión en (B) tenemos:
P2 – (M1 . a + P1) = M2 . a
P2 – P1 = M2 . a + M1 . a
Sacando a como factor común:
P2 – P1 = a . (M2 + M1)
Despejando nos queda:
Calculemos por separado P1 y P2
P1 = M1 . g = 3 Kg . 9,8 m/s2
P1 = 29,4 N
P2 = M2 . g = 5 Kg. . 9,8 m/s2
P2 = 49 N
Sustituyendo todos los valores conocidos en la expresión (C) nos queda que:
La tensión la obtenemos sustituyendo en la expresión:
T = M1 . a + P1
T = 3 Kg . 2,45 m/s2 + 29,4 N
T = 7,35 N + 29,4 N
T = 36,4 N
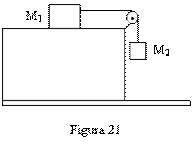
- 3. En la figura 21 se muestran dos bloques de masa M2 = 2 Kg. que arrastra sobre el plano horizontal al cuerpo de masa M1 = 7 Kg. Calcular la aceleración del sistema y tensión de la cuerda.
Solución
Antes debemos hacer un diagrama del cuerpo libre.
Para el bloque horizontal se muestra la figura 21(a) y para el bloque vertical el diagrama de la figura 21(b).

Horizontalmente se desplaza hacia la derecha y la única fuerza que actúa es la tensión, por lo que puede escribirse de acuerdo con la segunda ley de Newton que:
T = M1 . a.………………………….…………….….… (I)
En el bloque de masa M2, se lleva a cabo un movimiento vertical hacia abajo, pudiéndose escribir que:
P2 – T = M2 . a.………………………………………… (II)
Sustituyendo T de la ecuación (I) en (II) se tiene:
P2 – M1 . a = M2 ( a
Transponiendo términos se tiene que:
P2 = M2 . a + M1 ( a
Sacando a como factor común:
P2 = a . (M2 + M1)
Despejando nos queda:
Sustituyendo todos los valores conocidos en la expresión (C) nos queda que:
La tensión de la cuerda la obtenemos sustituyendo en la expresión:
T = M1 . a = 2Kg. ( 2,17 m/s2
T = 4,34 N
Ley de gravitación universal.
- 1. Hallar la fuerza con que se atraen dos masas de 5,5 ( 1024 Kg. y 7,3 ( 1022 Kg. separados por una distancia de 3,8 ( 108 m.
Solución
F = ?
M1 = 5,5 . 1024 Kg.
M2 = 7,3 . 1022 Kg.
d = 3,8 . 108 m
Para calcular la fuerza de atracción entre las masas M1 y M2, sustituimos en la fórmula de la cuarta ley de Newton el valor de cada una de ellas, así como los valores de G, y de la distancia d:
Quedando la fórmula como sigue:
- 2. Calcular la masa de un cuerpo, si fuerza de atracción entre dos masas es de 1,8 ( 10-2 N y la masa de una de ellas 0,6 ( 102 Kg., y las separa una distancia de 0,2 ( 10-1 m.
Solución
F = 1,8 ( 10-2 N
M1 = 0,6 ( 102 Kg.
M2 =?
d = 0,2 ( 10-1 m
Despejando M2 de la fórmula de la cuarta ley de Newton tenemos
Sustituyendo en la fórmula los valores tenemos:
PRIMERA CONDICIÓN DE EQUILIBRIO
PRIMERA CONDICIÓN DEL EQUILIBRIO. Consideremos un objeto que cuelga de una cuerda, como se muestra en la figura. Sobre el objeto actúan dos fuerzas: una de ellas es la tensión de la cuerda que impide que el objeto caiga, la otra es la fuerza de gravedad, la cual actúa sobre el objeto atrayéndolo hacia abajo, a dicha fuerza la definimos como el peso del objeto.
En resumen tenemos que:
REGLAS PARA RESOLVER PROBLEMAS APLICANDO LA PRIMERA CONDICIÓN DEL EQUILIBRIO:
1. Considere todas las fuerzas que actúan sobre el cuerpo en cuestión.
2. Traza un diagrama de cuerpo libre y establece un sistema de coordenadas cartesianas.
3. Lleva a cabo la descomposición de las fuerzas sobre los ejes X y Y.
4. Iguala a cero la suma algebraica de las componentes escalares sobre cada eje (primera condición del equilibrio).
5. Resuelve el sistema de ecuaciones resultante
 ROZAMIENTO O FRICCIÓN
ROZAMIENTO O FRICCIÓN
La fuerza de fricción o la fuerza de rozamiento es la fuerza que existe entre dos superficies en contacto, que se opone al movimiento relativo entre ambas superficies (fuerza de fricción dinámica) o a la fuerza que se opone al inicio del deslizamiento (fuerza de fricción estática). Se genera debido a las imperfecciones, mayormente microscópicas, entre las superficies en contacto. Estas imperfecciones hacen que la fuerza perpendicular R entre ambas superficies no lo sea perfectamente, sino que forme un ángulo con la normal N (el ángulo de rozamiento). Por tanto, la fuerza resultante se compone de la fuerza normal N (perpendicular a las superficies en contacto) y de la fuerza de rozamiento F, paralela a las superficies en contacto.
Rozamiento entre superficies de dos sólidos
En el rozamiento entre dos cuerpos se ha observado los siguientes hechos:
- La fuerza de rozamiento tiene dirección paralela a la superficie de apoyo.
- El coeficiente de rozamiento depende exclusivamente de la naturaleza de los cuerpos en contacto, así como del estado en que se encuentren sus superficies.
- La fuerza máxima de rozamiento es directamente proporcional a la fuerza normal que actúa entre las superficies de contacto.
- Para un mismo par de cuerpos (superficies de contacto), el rozamiento es mayor un instante antes de que comience el movimiento que cuando ya ha comenzado (estático Vs. cinético).
El rozamiento puede variar en una medida mucho menor debido a otros factores:
- El coeficiente de rozamiento es prácticamente independiente del área de las superficies de contacto.
- El coeficiente de rozamiento cinético es prácticamente independiente de la velocidad relativa entre los móviles.
- La fuerza de rozamiento puede aumentar ligeramente si los cuerpos llevan mucho tiempo sin moverse uno respecto del otro ya que pueden sufrir atascamiento entre sí.
Algunos autores sintetizan las leyes del comportamiento de la fricción en los siguientes dos postulados básicos:1
- La resistencia al deslizamiento tangencial entre dos cuerpos es proporcional a la fuerza normal ejercida entre los mismos.
- La resistencia al deslizamiento tangencial entre dos cuerpos es independiente de las dimensiones de contacto entre ambos.
La segunda ley puede ilustrarse arrastrando un bloque sobre una superficie plana. La fuerza de arrastre será la misma aunque el bloque descanse sobre la cara ancha o sobre un borde más angosto. Estas leyes fueron establecidas primeramente por Leonardo da Vinci al final del siglo XV, olvidándose después durante largo tiempo; posteriormente fueron redescubiertas por el ingeniero francés Amontons en 1699. Frecuentemente se les denomina también leyes de Amontons.
Tipos de fricción
Existen dos tipos de rozamiento o fricción, la fricción estática (Fe) y la fricción dinámica (Fd). El primero es la resistencia que se debe superar para poner en movimiento un cuerpo con respecto a otro que se encuentra en contacto. El segundo, es la resistencia, de magnitud considerada constante, que se opone al movimiento pero una vez que este ya comenzó. En resumen, lo que diferencia a un roce con el otro, es que el estático actúa cuando los cuerpos están en reposo relativo en tanto que el dinámico lo hace cuando ya están en movimiento.
La fuerza de fricción estática, necesaria para vencer la fricción homóloga, es siempre menor o igual al coeficiente de rozamiento entre los dos objetos (número medido empíricamente y que se encuentra tabulado) multiplicado por la fuerza normal. La fuerza cinética, en cambio, es igual al coeficiente de rozamiento dinámico, denotado por la letra griega , por la normal en todo instante.
No se tiene una idea perfectamente clara de la diferencia entre el rozamiento dinámico y el estático, pero se tiende a pensar que el estático es algo mayor que el dinámico, porque al permanecer en reposo ambas superficies pueden aparecer enlaces iónicos, o incluso microsoldaduras entre las superficies, factores que desaparecen en estado de movimiento. Este fenómeno es tanto mayor cuanto más perfectas son las superficies. Un caso más o menos común es el del gripaje de un motor por estar mucho tiempo parado (no solo se arruina por una temperatura muy elevada), ya que al permanecer las superficies, del pistón y la camisa, durante largo tiempo en contacto y en reposo, pueden llegar a soldarse entre sí.
Un ejemplo bastante común de fricción dinámica es la ocurrida entre los neumáticos de un auto y el pavimento en un frenado abrupto.
Como comprobación de lo anterior, se realiza el siguiente ensayo, sobre una superficie horizontal se coloca un cuerpo, y le aplica una fuerza horizontal F , muy pequeña en un principio, se puede ver que el cuerpo no se desplaza, la fuerza de rozamiento iguala a la fuerza aplicada y el cuerpo permanece en reposo, en la gráfica se representa en el eje horizontal la fuerza F aplicada, y en el eje vertical la fuerza de rozamiento Fr.
Entre los puntos O y A, ambas fuerzas son iguales y el cuerpo permanece estático; al sobrepasar el punto A el cuerpo súbitamente se comienza a desplazar, la fuerza ejercida en A es la máxima que el cuerpo puede soportar sin deslizarse, se denomina Fe o fuerza estática de fricción; la fuerza necesaria para mantener el cuerpo en movimiento una vez iniciado el desplazamiento es Fd o fuerza dinámica, es menor que la que fue necesaria para iniciarlo (Fe). La fuerza dinámica permanece constante.
Si la fuerza de rozamiento Fr es proporcional a la normal N, y a la constante de proporcionalidad se la llama :
Y permaneciendo la fuerza normal constante, se puede calcular dos coeficientes de rozamiento: el estático y el dinámico como:
donde el coeficiente de rozamiento estático corresponde al de la mayor fuerza que el cuerpo puede soportar inmediatamente antes de iniciar el movimiento y elcoeficiente de rozamiento dinámico corresponde a la fuerza necesaria para mantener el cuerpo en movimiento una vez iniciado.
Fricción estática
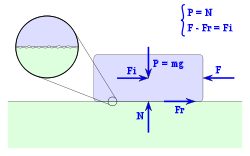
Es la fuerza que se opone al inicio del deslizamiento. Sobre un cuerpo en reposo al que se aplica una fuerza horizontal F, intervienen cuatro fuerzas:
- F: la fuerza aplicada.
- Fr: la fuerza de rozamiento entre la superficie de apoyo y el cuerpo, y que se opone al deslizamiento.
- P: el peso del propio cuerpo, igual a su masa por la aceleración de la gravedad.
- N: la fuerza normal, con la que la superficie reacciona sobre el cuerpo sosteniéndolo.
Dado que el cuerpo está en reposo la fuerza aplicada y la fuerza de rozamiento son iguales, y el peso del cuerpo y la normal:
Se sabe que el peso del cuerpo P es el producto de su masa por la aceleración de la gravedad (g), y que la fuerza de rozamiento es el coeficiente estático por la normal:
esto es:
La fuerza horizontal F máxima que se puede aplicar a un cuerpo en reposo es igual al coeficiente de rozamiento estático por su masa y por la aceleración de la gravedad.
Rozamiento dinámico
Dado un cuerpo en movimiento sobre una superficie horizontal, deben considerarse las siguientes fuerzas:
- Fa: la fuerza aplicada.
- Fr: la fuerza de rozamiento entre la superficie de apoyo y el cuerpo, y que se opone al deslizamiento.
- P: el peso del propio cuerpo, igual a su masa por la aceleración de la gravedad.
- N: la fuerza normal, que la superficie hace sobre el cuerpo sosteniéndolo.
Como equilibrio dinámico, se puede establecer que:
Sabiendo que:
prescindiendo de los signos para tener en cuenta solo las magnitudes, se puede reescribir la segunda ecuación de equilibrio dinámico como:
Es decir, la fuerza de empuje aplicada sobre el cuerpo es igual a la fuerza resultante menos la fuerza de rozamiento que el cuerpo opone a ser acelerado. De esa esa misma expresión se deduce que la aceleración que sufre el cuerpo, al aplicarle una fuerza Fa mayor que la fuerza de rozamiento Fr con la superficie sobre la que se apoya.
 . Esta expresión es una ecuación vectorial, ya que tanto la fuerza como la aceleración llevan dirección y sentido. Por otra parte, cabe destacar que la aceleración no es la variación de la posición, sino que es la variación con la que varía la velocidad.
. Esta expresión es una ecuación vectorial, ya que tanto la fuerza como la aceleración llevan dirección y sentido. Por otra parte, cabe destacar que la aceleración no es la variación de la posición, sino que es la variación con la que varía la velocidad.













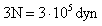


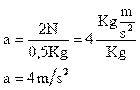

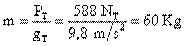
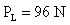


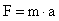

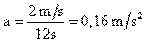

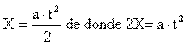
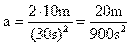
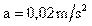



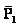





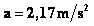
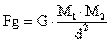



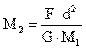
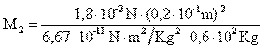
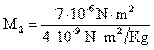











 , por la normal en todo instante.
, por la normal en todo instante.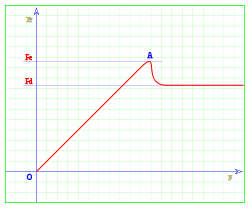


 corresponde al de la mayor fuerza que el cuerpo puede soportar inmediatamente antes de iniciar el movimiento y elcoeficiente de rozamiento dinámico
corresponde al de la mayor fuerza que el cuerpo puede soportar inmediatamente antes de iniciar el movimiento y elcoeficiente de rozamiento dinámico  corresponde a la fuerza necesaria para mantener el cuerpo en movimiento una vez iniciado.
corresponde a la fuerza necesaria para mantener el cuerpo en movimiento una vez iniciado.