Cinemática
Temas de física
- 1. MRU, MOVIMIENTO, DISTANCIA, DESPLAZAMIENTO, TRAYECTORIA, RAPIDOS Y VELOCIDAD.
- 2. PROBLEMAS DE MOVIMIENTO RECTILINEO UNUFORME
- 3. DEFINIRA MRUA, ACELERACIÒN Y DESACELERACIÒN
- 4. PROBLEMAS DE MOVIMIENTO RECTILINEO UNUFORMEMENTE ACELERADO
- 5. Definirá CAÌDA LIBRE Y TIRO VERTICAL
- 6. PROBLEMAS DE CAÌDA LIBRE Y TIRO VERTICAL
- 7. Definirá movimientos de proyectiles (horizontal y parabólico)
- 8. Resolverá problemas de proyectiles
- 9. Definirá movimiento circular, aceleración, aceleración y fuerzas centrípetas
- 10. Problemas de movimiento circular uniforme
- 11. Definirá mcua, desplazamiento, velocidad y aceleración angular.
- 12. Problemas de movimiento angular.
MRU
(MOVIMIENTO RECTILINEO UNIFORME)
¿QUÉ ES MOVIMIENTO RECTILINEO UNIFORME?
Un movimiento es rectilíneo cuando un objeto
describe una trayectoria recta, y es uniforme cuando su velocidad es constante en el tiempo, dado que su aceleración es nula. Es indicado mediante el acrónimo MRU.
- Movimiento que se realiza sobre una línea recta.
- Velocidad constante; implica magnitud y dirección constantes.
- La magnitud de la velocidad recibe el nombre de celeridad o rapidez.
- Aceleración nula.
PROPIEDADES Y CARACTERÍSTICAS
La distancia recorrida se calcula
multiplicando la magnitud de la velocidad por el tiempo transcurrido. Esta
relación también es aplicable si la trayectoria no es rectilínea, con tal que
la rapidez o módulo de la velocidad sea
constante. Por lo tanto el movimiento puede considerarse en dos sentidos; una
velocidad negativa representa un movimiento en dirección contraria al sentido
que convencionalmente hayamos adoptado como positivo.
De acuerdo con la Primera Ley de Newton, toda partícula permanece en reposo o
en movimiento rectilíneo uniforme cuando no hay una fuerza externa que actúe
sobre el cuerpo, dado que las fuerzas actuales están en equilibrio, por lo cual
su estado es de reposo o de movimiento rectilíneo uniforme. Esta es una
situación ideal, ya que siempre existen fuerzas que tienden a alterar el
movimiento de las partículas, por lo que en el movimiento rectilíneo uniforme
(MRU) es difícil encontrar la fuerza amplificada.
Representación gráfica del movimiento
Al representar gráficamente en un sistema de coordenadas cartesianas, la velocidad en
función del tiempo se obtiene una recta paralela al eje de abscisas (tiempo).
Además, el área bajo la recta producida representa la distancia
recorrida.
La representación gráfica de la
distancia recorrida en función del tiempo da lugar a una recta cuya pendiente se corresponde
con la velocidad.
Ecuaciones
del M.R.U
v=d/t
Donde
v: velocidad
d: distancia
t: tiempo
¿QUÉ ES MOVIMIENTO?
El movimiento es un cambio de posición respecto del
tiempo medido por un cierto observador.
El estudio del movimiento se
puede realizar a través de la cinemática o a través de la dinámica. En función
de la elección del sistema de referencia quedarán definidas las ecuaciones del
movimiento, ecuaciones que determinarán la posición, la velocidad y la
aceleración del cuerpo en cada instante de tiempo. Todo movimiento puede
representarse y estudiarse mediante gráficas. Las más habituales son las que
representan el espacio, la velocidad o la aceleración en función del tiempo.
Un sistema físico real se caracteriza
por, al menos, tres propiedades importantes:
El movimiento se refiere al cambio de ubicación en el espacio a lo largo del tiempo, tal como es medido por un observador físico. Un poco más generalmente el cambio de ubicación puede verse influido por las propiedades internas de un cuerpo o sistema físico, o incluso
el estudio del movimiento en toda su
generalidad lleva a considerar el cambio de dicho estado físico.
La
descripción del movimiento de los cuerpos físicos se denomina cinemática (que solo se ocuparía de las propiedades 1 y 2 anteriores). Esta disciplina pretende describir el modo en que un determinado cuerpo se mueve y qué propiedades tiene dicho movimiento. La física clásica nació estudiando la cinemática de cuerpos rígidos.
descripción del movimiento de los cuerpos físicos se denomina cinemática (que solo se ocuparía de las propiedades 1 y 2 anteriores). Esta disciplina pretende describir el modo en que un determinado cuerpo se mueve y qué propiedades tiene dicho movimiento. La física clásica nació estudiando la cinemática de cuerpos rígidos.
DISTANCIA
¿Qué ES?
En matemáticas, la distancia entre dos
puntos del espacio euclídeo equivale a la longitud del segmento de la recta que los
une, expresado numéricamente. En espacios más complejos, como los definidos en
la geometría no euclidiana, el
«camino más corto» entre dos puntos es un segmento recto con curvatura llamada geodésica.
Del latín distantia, la distancia es el trayecto espacial o el periodo temporal que separa dos acontecimientos o cosas. Se trata de la proximidad o
lejanía que existe entre objetos o eventos.
La distancia se refiere a cuanto espacio
recorre un objeto durante su movimiento. Es la cantidad movida.
También se dice que es la suma de las distancias recorridas. Por ser una
medida de longitud, la distancia se expresa en unidades de metro según el Sistema
Internacional de Medidas. Al
expresar la distancia, por ser una cantidad escalar, basta con mencionar la
magnitud y la unidad. Imagina que comienzas a caminar siguiendo la
trayectoria: ocho metros al norte, doce metros al este y finalmente ocho metros
al sur. Luego del recorrido, la distancia total recorrida será de 28
metros. El número 28 representa la magnitud de la distancia recorrida.
DESPLAZAMIENTO
El desplazamiento se refiere
a la distancia y la dirección de la posición final respecto a la posición
inicial de un objeto. Al igual que la distancia, el desplazamiento es una
medida de longitud por lo que el metro es la unidad de medida. Sin embargo, al
expresar el desplazamiento se hace en términos de la magnitud con su respectiva
unidad de medida y la dirección. El desplazamiento es una cantidad de tipo
vectorial. Los vectores se describen a partir de la magnitud y de la dirección. Vamos
a considerar la misma figura del ejemplo anterior.
Observa que recorres 8m en dirección Norte, luego 12 m en
dirección Este y por último 8 m en dirección Sur. Para el desplazamiento
solo importa el punto de inicio y el punto final por lo que el vector
entrecortado muestra el desplazamiento. El resultado es 12m en dirección
Este. Para esto recorres una distancia de 28m.
Matemáticamente, el desplazamiento (Δd) se calcula como:
df – di = Δd
Donde df es la posición final y di es la posición inicial del
objeto. El signo del resultado de la operación indica la dirección del
desplazamiento según el sistema de coordenadas definido. En el caso
anterior, el desplazamiento hubiese sido +12m al este.
Cuando el objeto termina en el mismo lugar de inicio el
desplazamiento será cero aunque la distancia no necesariamente lo sea. A
esta trayectoria en la que la posición final e inicial son iguales, se conoce
como un paso cerrado. El cambio en la posición de un objeto también se puede
representar gráficamente. Las características de la gráfica son parámetros que
nos ayudan a describir el movimiento del objeto bajo estudio. El tema de análisis
gráfico del movimiento rectilíneo
que discutimos anteriormente te puede ayudar a entender el concepto básico de vectores.
TRAYECTORIA
por las que pasa un cuerpo en su movimiento. La trayectoria depende del sistema de
referencia en el que
se describa el movimiento; es decir el punto de vista del observador.
La trayectoria de un cuerpo es, por lo general, una línea que goza de continuidad
RÁPIDOS Y VELOCIDAD
La rapidez o celeridad promedio es
la relación entre la distancia recorrida y el tiempo empleado en completarla.
Su magnitud se designa como v.
La celeridad es una magnitud escalar de
dimensión [L]/ [T]. La
rapidez tiene la misma dimensión que la velocidad, pero no
el carácter vectorial de esta.
La celeridad instantánea representa justamente el módulo de la
velocidad instantánea. La diferencia entre velocidad y rapidez es que la
velocidad tiene un carácter vectorial y la rapidez es una magnitud de carácter
escalar.
Aunque los términos de celeridad o rapidez son apropiados cuando deseamos
referirnos inequívocamente al módulo de la velocidad, es correcto y de uso
corriente (no sólo en el uso popular, sino también en el científico y técnico)
utilizar los términos "velocidad", "celeridad" y
"rapidez" como sinónimos. Esto es así para la totalidad de las
magnitudes vectoriales (aceleración, fuerza, momento, cantidad de movimiento,
etc.) a cuyos módulos no se les asigna nombres especiales
La rapidez es una
magnitud escalar que solo indica la magnitud de la velocidad. Por ejemplo,
supongamos que un felino puede desarrollar una velocidad de 90 km/h, mientras
que un atleta de alto rendimiento puede desarrollar una velocidad de 30 km/h,
podemos decir, tomando como referencia las velocidades, que el felino es 3
veces más rápido que el atleta.
Definición de
los vectores velocidad media e instantánea.
Definición de
celeridad media:
Definición de
velocidad instantánea y de celeridad instantánea:
Donde dr es
el vector desplazamiento y ds es
la distancia medida sobre la trayectoria, asociada al desplazamiento.
Podemos expresar el
vector velocidad en la forma
Donde et es
el vector unitario en la dirección
de la velocidad, tangente a la trayectoria, por lo que recibe el nombre
de versor tangente.
Los velocímetros de que disponen los vehículos
miden el módulo de la velocidad instantánea, esto es, la celeridad.
Un objeto en
movimiento recorre una cierta distancia en un tiempo determinado. Un auto, por
ejemplo, recorre un cierto número de kilómetros en una hora. La rapidez es una
medida de que tán aprisa se mueve un objeto. Es la razón de cambio a la que se
recorre la distancia. Recuerda que la expresión razón de cambio indica que
estamos dividiendo alguna cantidad entre el tiempo. La rapidez se mide siempre
en términos de una unidad de distancia dividida entre una unidad de tiempo. La
rapidez se define como la distancia recorrida por unidad de tiempo. Aquí la
palabra "por" significa "dividido entre" y la rapidez
describe cuán rápido se desplaza un objeto.
b) El tipo de movimiento
es rectilíneo uniforme porque la velocidad permanece constante durante toda la
carrera.
c) A los 4 s el corredor
recorrió 20 m.
Problema 3.- Un barco recorre la
distancia que separa Gran Canaria de Tenerife (90 km) en 6 horas. ¿Cuál es la
velocidad del barco en km/h? ¿Y en m/s?
Como la fórmula de la velocidad en
el MRU es v = d/t, la velocidad del barco será:
v =
d/t = 90/6 = 15 Km/h
Para pasar a metros por segundo,
multiplicamos por 1000 (porque un kilómetro son 1000 metros) y dividimos entre
3600 (porque una hora son 3600 segundos):
15·1000/3600
= 4,17m/s
Problema 4.- ¿Cuánto tiempo
tardaré en completar la distancia de una maratón (42 km) si corro a una
velocidad media de 15 km/h?
Igual que el anterior, solo que en esta
ocasión la incógnita es el tiempo en lugar de la velocidad:
v =
d/t 15 = 42/t
t = 42/15 = 2,8 horas
PROBLEMA 5.- Un avión vuela a una
velocidad de 900 km/h. Si tarda en viajar desde Canarias hasta la península 2
horas y media, ¿qué distancia recorre en ese tiempo?
Igual que los anteriores, pero ahora la
incógnita es la distancia. Recuerda que “dos horas y media” tenemos que
indicarlo con una única cifra decimal que sería 2,5 horas:
v =
d/t 900 = d/2,5
d = 900·2,5
= 2250Km
MRUA
(MOVIMIENTO RECTILÍNEO UNIFORMEMENTE ACELERADO)
El movimiento
rectilíneo uniformemente acelerado (MRUA), también conocido como movimiento
rectilíneo uniformemente variado (MRUV), es aquel en el que
un móvil se desplaza sobre una trayectoria recta estando sometido a una aceleración constante.
También
puede definirse como el movimiento que realiza una partícula que partiendo del
reposo es acelerada por una fuerza constante.
El
movimiento rectilíneo uniformemente acelerado (MRUA) es un caso particular
del movimiento uniformemente acelerado (MUA).
ACELERACIÒN
En
la FISICA, la aceleracion es una magnitud vectorial que nos indica la variacion
de velocidad por unidad de tiempo. En
el contexto de la mecánica vectorial newtoniana se representa
normalmente por o y su módulo por . Sus dimensiones son . Su unidad en el Sistema Internacional es m/s2.
El concepto
aceleración, no tiene que ver con ir moviéndose rápido. Es un concepto
que en muchas ocasiones ha sido mal utilizado en la vida real, sin embargo, su
significado en física es muy diferente. Es muy común escuchar
que se utiliza este concepto para indicar que un objeto se mueve a gran
velocidad lo cual es incorrecto.
El concepto aceleración se refiere al
cambio en la velocidad de un objeto. Siempre que un objeto cambia su
velocidad, en términos de su magnitud o dirección, decimos que está
acelerando.
DESACELERACIÓN
Es la
variación negativa de la velocidad, o sea la magnitud física que expresa el
paso de un cuerpo en movimiento de una velocidad a otra velocidad inferior,
siguiendo siempre la misma trayectoria. Dicho término puede definirse también
como aceleración negativa.
FÒRMULAS DE MRUA
e
= espacio recorrido
t = tiempo transcurrido
V0 = velocidad inicial
Vf = velocidad final
a = aceleración
enº = distancia o espacio recorrido en el n–ésimo segundo.
2.- La velocidad de un
vehículo aumenta uniformemente desde 15 km/h hasta 60 km/h en 20 s.
Calcular:
a) la velocidad media en km/h y en m/s, b) la
aceleración, c) la distancia, en metros, recorrida durante este tiempo.
Recuerde que para transformar de km/h a m/s hay que dividir por 3,6.
Datos:
vi = 15 (km/h) = 4,167
(m/s)
vf = 60 (km/h) = 16,67 (m/s)
t = 20 (s)
a = (vf – vi)/t = (16,67 (m/s) -
4,167 (m/s))/20 (s) = 0,625 (m/s2 )
d = vit + at2 /2 = 4,167 (m/s) x 20 (s) +
0,625 (m/s2 ) x (20 (s))2 /2
= 208,34 (m)
3.- Un vehículo que marcha a una velocidad de 15 m/s
aumenta su velocidad a razón de 1 m/s cada segundo.
a) Calcular la
distancia recorrida en 6 s.
b) Si disminuye su velocidad a razón de 1 m/s cada
segundo, calcular la distancia recorrida en 6 s y el tiempo que tardará en
detenerse.
Datos:
vi = 15
(m/s)
a = 1 (m/s2 )
a) d = vit + at2 /2 = 15 (m/s) x 6 (s) + 1 (m/s2 ) x (6
(s))2 /2
= 108 (m)
b) d = vit + at2 /2 = 15 (m/s) x 6 (s) + 1 (m/s2 ) x (-6
(s))2 /2 = 72 (m)
t = (vf – vi)/a = (0 (m/s) – 15 (m/s))/(-1 (m/s2 ))
= 15 (s)
4.- Un automóvil que marcha a una velocidad de 45
km/h, aplica los frenos y al cabo de 5 s su velocidad se ha reducido a 15 km/h.
Calcular
a) la aceleración
b) la distancia recorrida durante
los cinco segundos.
Datos:
vi = 45 (km/h) = 12,5 (m/s)
vf = 15 (km/h) =
4,167 (m/s)
t = 5 (s) a = (vf – vi)/t = (4,167 (m/s) – 12,5 (m/s))/5 (s)
=
-1,67 (m/s2 ) d = vit + at2 /2
= 12,5 (m/s) x 5 (s) + (-1,67 (m/s2 )) x (5
(s))2 /2
= 41,625 (m)
5.- La velocidad de un tren se reduce uniformemente de
12 m/s a 5 m/s. Sabiendo que durante ese tiempo recorre una distancia de 100 m.
Calcular
a) la
aceleración
b) la distancia
que recorre a continuación hasta detenerse suponiendo la misma aceleración.
Datos:
vi = 12 (m/s)
vf = 5 (m/s) d = 100 (m)
a) a = (vf 2 –
vi 2 )/2d = ((5(m/s))2 – (12 (m/s))2 /(2 x 100 (m)) = - 0,595 (m/s2)
b) d = (vf 2 –
vi 2 )/2a
= ((0(m/s))2 – (12 (m/s))2 /(2 x (-0,595 (m/s2 )))
= 121 (m)
CAÍDA LIBRE
En física, se denomina caída libre al movimiento de un
cuerpo bajo la acción exclusiva de un campo gravitatorio. Esta definición
formal excluye a todas las caídas reales influenciadas en mayor o menor medida
por la resistencia
aerodinámica del aire, así como a
cualquier otra que tenga lugar en el seno de un fluido; sin embargo, es frecuente también
referirse coloquialmente a éstas como caídas libres, aunque los efectos de
la viscosidad del medio no
sean por lo general despreciables.
El concepto es aplicable también a objetos en
movimiento vertical ascendente sometidos a la acción desaceleradora de la gravedad, como un disparo vertical; o a cualquier objeto (satélites naturales o artificiales, planetas, etc.) en órbita alrededor de
un cuerpo celeste. Otros sucesos
referidos también como caída libre lo constituyen las trayectorias geodésicas en el espacio-tiempo descritas en la teoría de
la relatividad general.
Ejemplos de caída libre deportiva los
encontramos en actividades basadas en dejarse caer una persona a través de
la atmósfera sin sustentación alar ni de paracaídas durante un cierto trayecto.
Un sistema de referencia ligado a un
cuerpo en caída libre puede considerarse inercial o no
inercial en función del marco teórico que se esté usando.
En la física clásica, la fuerza gravitatoria que se ejerce
sobre una masa es proporcional a la intensidad
del campo gravitatorio en la
posición espacial donde se encuentre dicha masa. La constante de
proporcionalidad es precisamente el valor de la masa inercial del cuerpo, tal y como
establece el principio
de equivalencia. En la física relativista, la gravedad es el
efecto que produce sobre las trayectorias de los cuerpos la curvatura del espacio-tiempo; en este caso, la gravedad no es una
fuerza, sino una geodésica. Por tanto, desde el punto de vista
de la física clásica, un sistema de
referencia en caída libre es un sistema acelerado por la fuerza de la gravedad
y, como tal, es no inercial. Por el contrario, desde el punto de vista de
la física relativista, el mismo sistema
de referencia es inercial, pues aunque está acelerado en el espacio, no está
acelerado en el espacio-tiempo. La diferencia radica en la propia definición
de los conceptos geométricos y cinemáticos, que para cada marco teórico son
completamente diferentes.
FÒRMULAS
DE CAÌDA LIBRE
Tiro vertical
La noción
de tiro vertical aparece en el
campo de la física. Se trata de un movimiento rectilíneo uniforme variado, también
conocido como MRUV. En un tiro vertical, la
velocidad cambia y existe una aceleración que está dada por la acción de la
gravedad.
El tiro
vertical, cuya dirección puede ser descendente o ascendente, tiene una velocidad inicial que
resulta diferente a cero. El cuerpo en cuestión se lanza hacia arriba,
impulsado con una cierta velocidad. Luego regresa al punto de partida con la
misma velocidad, aunque en un sentido contrario a la que tenía en el momento
del lanzamiento.
Puede
decirse, de este modo, que el cuerpo lanzado en un tiro vertical sube y luego baja, regresando al punto
de partida. Cuando el cuerpo alcanzó la altura
máxima, la velocidad resulta nula.
En ese instante, el cuerpo deja de subir e inicia su descenso. El tiempo que el
cuerpo demora en llegar a la altura máxima resulta idéntico al tiempo que tarda
en volver a su punto de partida.
Es importante
destacar que existen diversas ecuaciones que
permiten medir diferentes magnitudes vinculadas al tiro vertical. Estas
ecuaciones trabajan con variables como la velocidad
inicial, la altura y la aceleración.
Un ejemplo de
tiro vertical se produce cuando tomamos una pelota
de tenis con una mano y la lanzamos hacia arriba en línea recta.
Dicha pelota subirá durante una breve fracción de tiempo, llegará a su altura máxima y luego descenderá, volviendo a nuestra
mano. En la práctica, de todos modos, el tiro vertical puede resultar
complicado de realizar ya que el lanzamiento puede no ser recto, el viento
puede influir en la pelota, etc.
PROBLEMAS DE CAÌDA LIBRE Y TIRO VERTÌCAL
CAÌDA LIBRE
PROBLEMA 1
MOVIMIENTO DE PROYECTILES
(HORIZONTAL Y PARÀBOLICO)
Lanzamiento Horizontal
El lanzamiento horizontal es un tipo
de movimiento que explica la interacción que tiene un
"móvil" al estar en movimiento con una serie de factores físicos.
Este móvil durante su trayectoria tiene una serie
de características específicas que lo diferencia de otro tipo de
movimiento. Dichas características son:
* Tiene una relación directa con la
"caída libre", la cual según Brett C., E., Suárez, W. A. (2012)
"es el movimiento, en dirección vertical, con aceleración constante
realizado por un cuerpo cuando se deje caer en el vacío".
* Este tipo de lanzamiento combina
dos tipos de movimientos: el vertical (producido por la caída libre) y el
vertical (definido como un Movimiento Rectilíneo Uniforme).
* Ya que tiene dos movimientos, uno
que atrae (la gravedad), y otro que hace mover al móvil hacia un lado
“horizontal” (MRU), tenemos que la trayectoria es una semiparábola.
* Sí presenta un movimiento de caída libre, tenemos que la aceleración es la gravedad, la cual es: 9.8 m/s2.
* La Velocidad Inicial tiene solo
componente horizontal, ya que la misma es accionada en sentido “horizontal”
(valga la redundancia).
* La Velocidad dependerá de la altura
del lanzamiento.
La velocidad es aquella “distancia”
que recorre el móvil en cierta cantidad de tiempo. Básicamente se calcula
dividiendo la distancia recorrida entre el tiempo en que duro su trayecto. En
este caso, tenemos dos tipos de velocidades en este lanzamiento, la velocidad
“Vx” y la velocidad “Vy”.
La velocidad en “x” (Vx) se calcula
de la siguiente manera:
Vo = Vx = x /
t (x = distancia recorrida; t = tiempo)
La velocidad en “y” (Vy) se calcula
de la siguiente manera:
Vy = g t
(g = gravedad; t =
tiempo)
La velocidad cuadrar en “y” (Vy2)
se calcula de la siguiente manera:
Vy2 = 2 g t
El componente “y” o altura se calcula
de la siguiente manera:
Y = 0.5 g t2
Velocidad a cualquier instante
a) La magnitud de la
componente vertical de la velocidad
b) El tiempo
transcurrido
c) Cuanto ha
descendido
d) Cuanto ha recorrido
horizontalmente
e) Si la bomba tarda
10 segundos en dar en el blanco, calcular la altura del avión.
Se denomina movimiento parabólico al realizado por cualquier objeto cuya
trayectoria describe una parábola. Se corresponde con la trayectoria ideal de unproyectil que se mueve
en un medio que no ofrece resistencia al avance y que está sujeto a un campo gravitatorio uniforme. El movimiento
parabólico es un ejemplo de un movimiento realizado por un objeto en dos
dimensiones o sobre un plano. Puede considerarse como la combinación de dos movimientos
que son un movimiento horizontal uniforme y un movimiento vertical rectilíneo.
En realidad, cuando se habla de cuerpos que se
mueven en un campo gravitatorio central (como el de La Tierra), el movimiento
es elíptico. En la superficie
de la Tierra, ese movimiento es tan parecido a una parábola que perfectamente
podemos calcular su trayectoria usando la ecuación matemática de una parábola.
La ecuación de una elipse es bastante más compleja. Al lanzar una piedra al
aire, la piedra intenta realizar una elipse en uno de cuyos focos está el
centro de la Tierra. Al realizar esta elipse inmediatamente choca con el suelo
y la piedra se para, pero su trayectoria es en realidad un "trozo" de
elipse. Es cierto que ese "trozo" de elipse es casi idéntico a un
"trozo" de parábola. Por ello utilizamos la ecuación de una parábola
y lo llamamos "tiro parabólico". Si nos alejamos de la superficie de
la Tierra sí tendríamos que utilizar una elipse(como en el caso de los
satélites artificiales).
El movimiento parabólico puede ser analizado como
la composición de dos movimientos rectilíneos: un movimiento rectilíneo uniforme horizontal y
un movimiento rectilíneo uniformemente acelerado vertical.
- El tiro parabólico tiene las siguientes características:
- Conociendo la velocidad de salida (inicial), el ángulo de inclinación inicial y la diferencia de alturas (entre salida y llegada) se conocerá toda la trayectoria.
- Los ángulos de salida y llegada son iguales (siempre que la altura de salida y de llegada sean iguales)
- La mayor distancia cubierta o alcance se logra con ángulos de salida de 45º.
- Para lograr la mayor distancia fijado el ángulo el factor más importante es la velocidad.
ecuaciones del movimiento parabólico:
En la figura anterior sean V0 = 160 pies/s y 0 = 53.1o. En tal caso,
Vox = Vo cos o = (160 pies/s )(0.60)=96 pies/s
Voy = Vo sen o = (160 pies/s )(0.80)=128 pies/s
Determínese la posición del proyectil y la magnitud y dirección de su velocidad cuando t = 2.0 s.
x = (96 pies/s )(2.0 s)=192 pies
y = (128 pies/s )(2.0 s)-½(32 pies/s) (2.0 s )2 = 192 pies
vx = 96 pies/s
vy = 128 pies/s - (32 pies/s) (2.0 s ) = 64 pies/s
v = "vx2 + vy2 = 115.4 pies/s
= arctan 64 pies/s = arctan 0.667 = 33.7o
96 pies/s
Calcúlese el tiempo que tarda el proyectil en alcanzar el punto más elevado de su trayectoria y la altura de dicho punto.
En el punto más elevado, la velocidad vertical vy es cero. Si t1, es el instante en el que alcanza dicho punto,
Vy = 0 = 128 pies/s -(32 pies/s)t1
t1 = 4s
la altura h del punto es el valor de y cuando t = 4s.
h = (128 pies/s )(4 s)-½(32 pies/s) (4 s )2 = 256 pies
Hállese el alcance horizontal R, es decir, la distancia horizontal desde el punto de partida al punto en el que el proyectil vuelve a su altura inicial, esto es y = 0. Sea t2 el instante en el que alcanza este punto. Entonces
y = 0 = (128 pies/s ) t2 -½(32 pies/s) t22
Esta ecuación de Segundo grado tiene dos raíces:
t2 = 0 y t2 = 8 s
que corresponden a los dos instantes en los que y=0. Sin duda, el tiempo buscado es la segunda raíz, t2 = 8 s, que es exactamente el doble del tiempo empleado en alcanzar el punto más elevado. El tiempo de bajada es, por consiguiente, igual al de subida.
El alcance horizontal R es el valor de x cuando t = 8 s:
R = vx t2 = (96 pies/s)(8s) = 768 pies
La componente vertical de la velocidad en este punto es:
vy = (128 pies/s) - (32 pies/s) (8 s) = -128 pies/s
MOVIMIENTO CÌRCULAR
El movimiento circular es el que recorre una partícula o cuerpo por una circunferencia. Estemovimiento tiene un eje y todos los puntos por los que pasa la partícula se encuentran a una distancia constante (r) del eje.
En cinemática, el movimiento circular (también llamado movimiento circunferencial) es el que se basa en un eje de giro y radio constante, por lo cual la trayectoria es una circunferencia. Si además, la velocidad de giro es constante (giro ondulatorio), se produce el movimiento circular uniforme, que es un caso particular de movimiento circular, con radio y centro fijos y velocidad angular constante.
En el movimiento circular hay que tener en cuenta algunos conceptos básicos para la descripción cinemática y dinámica del mismo:
- Eje de giro: es la línea recta alrededor de la cual se realiza la rotación, este eje puede permanecer fijo o variar con el tiempo pero para cada instante concreto es el eje de la rotación (considerando en este caso una variación infinitesimal o diferencial de tiempo). El eje de giro define un punto llamado centro de giro de la trayectoria descrita (O).
- Arco: partiendo de un centro fijo o eje de giro fijo, es el espacio recorrido en la trayectoria circular o arco de radio unitario con el que se mide el desplazamiento angular. Su unidad es el radián (espacio recorrido dividido entre el radio de la trayectoria seguida, división de longitud entre longitud, adimensional por tanto).
- Velocidad angular: es la variación del desplazamiento angular por unidad de tiempo (omega minúscula,
 ).
). - Aceleración angular: es la variación de la velocidad angular por unidad de tiempo (alfa minúscula,
 ).
).
En dinámica de los movimientos curvilíneos, circulares y/o giratorios se tienen en cuenta además las siguientes magnitudes:
- Momento angular (L): es la magnitud que en el movimiento rectilíneo equivale al momento lineal o cantidad de movimiento pero aplicada al movimiento curvilíneo, circular y/o giratorio (producto vectorial de la cantidad de movimiento por el vector posición, desde el centro de giro al punto donde se encuentra la masa puntual).
- Momento de inercia (I): es una cualidad de los cuerpos que depende de su forma y de la distribución de su masa y que resulta de multiplicar una porción concreta de la masa por la distancia que la separa al eje de giro.
- Momento de fuerza (M): o par motor es la fuerza aplicada por la distancia al eje de giro (es el equivalente a la fuerza agente del movimiento que cambia el estado de un movimiento rectilíneo).
Aceleración
En física, la aceleración es una magnitud vectorial que nos indica la variación de velocidad por unidad de tiempo. En el contexto de la mecánica vectorial newtoniana se representa normalmente por  o
o  y su módulo por
y su módulo por  . Sus dimensiones son
. Sus dimensiones son ![\scriptstyle [ L \cdot T^{-2} ]](https://upload.wikimedia.org/math/8/d/9/8d93fafc52fa31cdcc17a888d15c7165.png) . Su unidad en el Sistema Internacional es m/s2.
. Su unidad en el Sistema Internacional es m/s2.
 o
o  y su módulo por
y su módulo por  . Sus dimensiones son
. Sus dimensiones son ![\scriptstyle [ L \cdot T^{-2} ]](https://upload.wikimedia.org/math/8/d/9/8d93fafc52fa31cdcc17a888d15c7165.png) . Su unidad en el Sistema Internacional es m/s2.
. Su unidad en el Sistema Internacional es m/s2.
En la mecánica newtoniana, para un cuerpo con masa constante, la aceleración del cuerpo es proporcional a la fuerza que actúa sobre el mismo (segunda ley de Newton):
donde F es la fuerza resultante que actúa sobre el cuerpo, m es la masa del cuerpo, y a es la aceleración. La relación anterior es válida en cualquier sistema de referencia inercial.
FUERZAS CENTRIPETAS
- Constante es un valor que no cambia y es distinto de cero.
- Se llama fuerza centrípeta a la fuerza, o al componente de la fuerza que actúa sobre un objeto en movimiento sobre una trayectoria curvilínea, y que está dirigida hacia el centro de curvatura de la trayectoria.
- El término «centrípeta» proviene de las palabras latinas centrum, «centro» y petere, «dirigirse hacia», y puede ser obtenida a partir de las leyes de Newton. La fuerza centrípeta siempre actúa en forma perpendicular a la dirección del movimiento del cuerpo sobre el cual se aplica. En el caso de un objeto que se mueve en trayectoria circular con velocidad cambiante, la fuerza neta sobre el cuerpo puede ser descompuesta en un componente perpendicular que cambia la dirección del movimiento y uno tangencial, paralelo a la velocidad, que modifica el módulo de la velocidad.
- La fuerza centrípeta no debe ser confundida con la fuerza centrífuga, tal como se explica en la sección Malentendidos comunes.
PROBLEMAS DE MCU
PROBLEMA 1.-
Un carro de juguete que se mueve con rapidez constante completa una vuelta alrededor de una pista circular (una distancia de 200 metros) en 25 seg.
a) Cual es la rapidez promedio?
b) Si la masa del auto es de 1,5 kg. Cual es la magnitud de la fuerza central que lo mantiene en un circulo?
a) Cual es la rapidez promedio?
b) Si la masa del auto es de 1,5 kg. Cual es la magnitud de la fuerza central que lo mantiene en un circulo? L = 200 metros = 2 π r
Despejamos el radio
F = 3,01 Newton
PROBLEMA 2.-
En un ciclotrón (un tipo acelerador de partículas), un deuterón (de masa atómica 2u ) alcanza una velocidad final de 10 % de la velocidad de la luz, mientras se mueve en una trayectoria circular de 0,48 metros de radio. El deuterón se mantiene en la trayectoria circular por medio de una fuerza magnética. Que magnitud de la fuerza se requiere?
Velocidad de la luz = 3 X 108 m/seg
Velocidad del deuterón = 3 X 107 m/seg
Masa deuterón 2u = 2 * 1,661 X 10-27 kg.
Masa deuterón 2u = 3,322 X 10-27 kg.
Una patinadora de hielo de 55 kg se mueve a 4 m/seg.. Cuando agarra el extremo suelto de una cuerda, el extremo opuesto esta amarrado a un poste.
Después se mueve en un circulo de 0,8 m de radio alrededor del poste.
a) Determine la fuerza ejercida por la cuerda sobre sus brazos.
b) Compare esta fuerza con su peso.
- Determine la fuerza ejercida por la cuerda sobre sus brazos.
T = 1100 Newton
b) Compare esta fuerza con su peso.
PROBLEMA 4.-
En el modelo de Bohr del átomo de hidrogeno, la rapidez del electrón es aproximadamente 2,2 * 106 m/seg. Encuentre:
a) La fuerza que actúa sobre el electrón cuando este gira en una orbita circular de 0,53 * 10- 10 metros de radio
b) la aceleración centrípeta del electrón.
Masa = 9,11 * 10- 31 Kg. V = 2,2 * 106 m/seg. r = 0,53 * 10- 10 metros
F = 83,192 * 10- 9 Newton
b) la aceleración centrípeta del electrón.
a = 9,132 * 1022 m/seg2
PROBLEMA 5.-
La velocidad de la punta de la manecilla de los minutos en el reloj de un pueblo es 1,75 * 10 -3 m/seg.
a) Cual es la velocidad de la punta de la manecilla de los segundos de la misma longitud?
b) Cual es la aceleración centrípeta de la punta del segundero?
(Tiempo del minutero) = tiempo en seg. Que demora en dar una vuelta completa el minutero al reloj
(Tiempo del minutero) = 60 minutos = 3600 seg.
(Tiempo del segundero) = tiempo en seg. Que demora en dar una vuelta completa el segundero al reloj
(Tiempo del segundero) = 60 seg.
Velocidad del minutero = 1,75 * 10 -3 m/seg.
Radio del minutero = radio del segundero
(Velocidad del minutero) * ( tiempo del minutero) = (Velocidad del segundero) * ( tiempo del segundero)
Velocidad del segundero = 0,105 m/seg.
b) Cual es la aceleración centrípeta de la punta del segundero?
Despejamos el radio.
V * t = 2 π r
MCUA
(MOVIMIENTO CIRCULAR
UNIFORMEMENTE ACELERADO)
El movimiento circular uniformemente acelerado (MCUA) se presenta cuando una partícula o cuerpo sólido describe una trayectoria circular aumentando o disminuyendo la velocidad de forma constante en cada unidad de tiempo. Es decir, la partícula se mueve con aceleración constante.
En el dibujo se observa un ejemplo en donde la velocidad aumenta linealmente en el tiempo. Suponiendo que el tiempo en llegar del punto P1 a P2 sea una unidad de tiempo, la partícula viaja con una aceleración tangencialuniforme v, incrementándose esa cantidad en cada unidad de tiempo.
Posición
El desplazamiento de la partícula es más rápido o más lento según avanza el tiempo. El ángulo recorrido (θ) en un intervalo de tiempo t se calcula por la siguiente fórmula:
Aplicando la fórmula del incremento de ángulo calculamos laposición en la que estará la partícula pasado un tiempo t se obtiene la fórmula de la posición:
Velocidad angular
La velocidad angular aumenta o disminuye linealmente cuando pasa una unidad del tiempo. Por lo tanto, podemos calcular la velocidad angular en el instante t como:
El sentido de la aceleración angular α puede ser contrario al de la velocidad angular ω. Si la aceleración angular es negativa, seria un caso de movimiento circular uniformemente retardado.
Velocidad tangencial
La velocidad tangencial es el producto de la velocidad angular por el radio r. La velocidad tangencialtambién se incrementa linealmente mediante la siguiente fórmula:
Dándose aquí igualmente la posibilidad de aceleración negativa que se ha descrito en el apartado anterior.
Aceleración angular
La aceleración angular en el movimiento circular uniformemente acelerado es constante. Se calcula como el incremento de velocidad angular ω desde el instante inicial hasta el final partido por el tiempo.
Aceleración tangencial
La aceleración tangencial en el movimiento circular uniformemente acelerado MCUA se calcula como el incremento de velocidad v desde el instante inicial hasta el final partido por el tiempo.
Aceleración centrípeta
La aceleración centrípeta en el MCUA se halla mediante:
Componentes intrínsecas de la aceleración
La velocidad tangencial por la trayectoria en un punto P es v. En un intervalo de tiempo pequeño Δt, la velocidad incrementa a v’ en el punto P’, después de haber descrito un ángulo Δφ.
En la figura se puede ver el incremento de la velocidad tangencial Δv descompuesta en dos componentes: la tangencial Δvt y la normal (o centrípeta) Δvn.
Si dividimos ambas componentes de la velocidad por Δt, tendremos las componentes intrínsecas de la aceleración: la aceleración tangencial at y la aceleración normal an (o centrípeta).
Período
En el MCUA la velocidad angular cambia respecto al tiempo. Por tanto, el período cada vez será menor o mayor según si decrece o crece la velocidad angular.
Frecuencia
La frecuencia en el caso del MCUA es mayor o menor porque la velocidad angular cambia. La fórmula de lafrecuencia será:
donde:
Unidades
d distancia de arco cm, m
θ desplazamiento angular rad
r radio cm, m
V velocidad lineal cm/s, m/s
ω velocidad angular rad/s
a aceleración lineal cm/s2
, m/s2
α aceleración angular rad/s2
1) Calcular la velocidad lineal de un disco de 30 cm de radio que tiene una velocidad
angular de 135 rad/s.
Datos Fórmula Sustitución Resultado
v= ωr v =135rad /s x 0.3m v = 40.5m/s
V= ?
ω = 135 rad/s
r = 30 cm =0.3m
problema 2.-
Cual es la rapidez máxima que el vehículo puede alcanzar en B y continuar sobre la pista.
Punto B Cuando el auto esta en la parte superior, la pista no ejerce fuerza sobre el vehiculo, es decir la normal en el punto máximo superior es cero.
∑ FY = m a
m g = m a
se cancela la masa.
V2 = g * r
V = 12,12 m/seg.
Cuando la normal es cero, la velocidad es máxima.
Un volante de 50cm de radio gira a 180 rpm. Si es frenado y se detiene en 20 segundos, calcula:
a) La velocidad angular inicial en radianes por segundo.
b) La aceleración de frenado.
c) El número de vueltas dadas en 20 segundos.
Ordenamos los datos:
R = 0,5 m
ω0 = 180rpm = 3π rad/s
ωf = 0 rad/s
t = 20 s
a) Ya lo hemos respondido al ordenar los datos.
Recuerda que para pasar de revoluciones por
minuto (rpm) a radianes por segundo, tenemos que dividir entre 60 y multiplicar por 2π (o hacer
una regla de tres sabiendo que 360º es igual a 2π radianes).
b) Para calcular la aceleración de frenado, usamos la fórmula de la velocidad en MCUA:
ωf = ω0 + α·t
0 = 3π + α·20
α = - 3π/20 rad/s2
Obviamente, la aceleración sale negativa porque el volante está frenando.
c) Para hallar el número de vueltas en esos 20 segundos, utilizamos la fórmula del arco o ángulo
recorrido del
MCUA:
φ = φ0 + ω0·t + 1/2·α·t2
φ = 3π ·20 - 1/2·3π/20 ·202
= 141,37 rad = 22,5 vueltas
PROBLEMA 4.-
4) Un hombre hace girar una honda desde el reposo durante 10 segundos con una aceleración
angular de π radianes/s2
, momento en el cual suelta la cuerda para dejar salir el proyectil. ¿A qué
velocidad sale despedido este si la cuerda de la honda mide 60cm?
ordenamos los datos:
t = 10s
α = π rad/s2
ω0= 0 rad/s
Primero tenemos que hallar la velocidad angular final al cabo de esos 10 segundos:
ωf = ω0 + α·t
ωf = π ·10 = 10π rad/s
Por lo que la velocidad lineal será:
v = 10π·0,6 = 18,85 m/s
PROBLEMA 5.-
5) ¿Cuánto tiempo tendría que hacer girar la honda el hombre del ejercicio anterior para que la
velocidad lineal de salida fuese del doble?
Ahora planteamos el problema "desde el final". Si la velocidad lineal final tiene que ser del doble,
v = 18,85·2 = 37,70 m/s
Por lo que la velocidad angular final debe ser:
v = ωf ·R
37,70 = ωf ·0,6
ωf = 62,83 rad/s
Y por lo tanto el tiempo será:
62,83 = 0 + π ·t
t = 20 segundos
































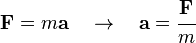
hola este es mi blog comenten que les parece por favor
ResponderBorrarespero y les guste
ResponderBorrar